Fraktal - definicja, właściwości, przykłady, zastosowania

Fraktale to jedne z najbardziej fascynujących obiektów matematycznych, łączące piękno, złożoność i głęboką strukturę ukrytą w prostych regułach. Choć termin "fraktal" został użyty dopiero w 1975 roku przez Benoîta Mandelbrota, koncepcja samopodobnych struktur była znana znacznie wcześniej.

Fraktale nie tylko zachwycają artystów i matematyków, ale odgrywają też istotną rolę w opisie zjawisk przyrodniczych, generowaniu krajobrazów komputerowych, analizie danych oraz modelowaniu chaosu. Czym zatem są fraktale i dlaczego zasługują na tak szeroką uwagę?

Czym jest fraktal? Definicja

Fraktale naturalne a matematyczne

• Fraktale matematyczne są precyzyjnie zdefiniowane i tworzone według ścisłych reguł - np. zbiór Mandelbrota, trójkąt Sierpińskiego, dywan Sierpińskiego, krzywa Kocha.
• Fraktale naturalne występują w przyrodzie jako przybliżone fraktale, np. kształt chmur, linie brzegowe, rozgałęzienia drzew czy układ naczyń krwionośnych.

Historia fraktali

Prekursorzy fraktali

• Karl Weierstrass (1872) - skonstruował funkcję ciągłą, ale nigdzie nie różniczkowalną.
• Georg Cantor (1883) - zaproponował zbiór Cantora, jeden z pierwszych przykładów fraktalnej struktury.
• Giuseppe Peano i David Hilbert - wprowadzili krzywe wypełniające przestrzeń.
• Helge von Koch (1904) - stworzył pierwszą klasyczną krzywą fraktalną.

W 1975 roku Benoît Mandelbrot, francusko-amerykański matematyk, opublikował książkę "Les Objets Fractals: Forme, Hasard et Dimension", w której po raz pierwszy użył słowa fraktal, pochodzącego od łacińskiego fractus (łamany). Mandelbrot zrewolucjonizował sposób postrzegania geometrii, wskazując, że klasyczna geometria Euklidesowa nie opisuje adekwatnie większości form przyrody.

Właściwości fraktali

1. Samopodobieństwo

Samopodobieństwo oznacza, że fraktal składa się z fragmentów przypominających całość. Każdy fragment, niezależnie od skali, odzwierciedla strukturę całego obiektu. W najprostszych przypadkach (np. trójkąt Sierpińskiego) samopodobieństwo jest dokładne i deterministyczne - mniejsze kopie są identyczne względem oryginału. W strukturach naturalnych (np. chmurach, drzewach, układzie naczyń) samopodobieństwo ma charakter statystyczny - nie jest idealne, ale zachowuje podobieństwo rozkładu. Istnieją też fraktale o tzw. samopodobieństwie afinicznym, gdzie fragmenty różnią się położeniem, skalą i kątem obrotu. Samopodobieństwo pozwala fraktalom być nieskończenie "rozbudowywanymi" bez zmiany ich struktury. To właśnie ta właściwość sprawia, że fraktale są efektywne w modelowaniu form przyrody i struktur danych. W grafice komputerowej wykorzystuje się ją do generowania krajobrazów i roślinności. W analizie danych pozwala wykrywać powtarzalne wzorce w szeregach czasowych. Matematycznie, samopodobieństwo jest podstawą do wyliczania wymiaru fraktalnego. To jedna z cech, które czynią fraktale jednocześnie prostymi w konstrukcji i niezwykle bogatymi w strukturę.

2. Nieskończona złożoność

Fraktale cechuje struktura, która pozostaje złożona przy dowolnym powiększeniu. Bez względu na to, jak bardzo się przybliży dany fragment fraktala, zawsze ukaże się kolejna warstwa detali. Oznacza to, że nie istnieje "najmniejszy" element fraktala - jego szczegółowość jest nieskończona. To przeciwieństwo klasycznych figur geometrycznych, które z bliska stają się gładkie. Nieskończona złożoność fraktali wynika często z bardzo prostych reguł generowania (np. rekurencji lub iteracji funkcji). Ta cecha pozwala na opisywanie procesów przyrodniczych i fizycznych, które działają na wielu skalach jednocześnie. Przykładami są turbulencje, struktura chmur, układ żył w liściach czy erozja terenu. Nieskończona złożoność czyni fraktale idealnymi do kompresji informacji - można zapisać bardzo złożony kształt prostym algorytmem. W matematyce pozwala to badać granice percepcji przestrzeni i wymiaru. W praktyce, tę cechę wykorzystuje się m.in. w sztuce generatywnej i analizie obrazów medycznych. Nieskończona złożoność sprawia, że fraktale można badać i eksplorować praktycznie bez końca - zawsze ukazuje się coś nowego.

3. Wymiar fraktalny

Wymiar fraktalny to liczba opisująca, jak "gęsto" fraktal wypełnia przestrzeń. W przeciwieństwie do klasycznego wymiaru (punkt = 0D, linia = 1D, płaszczyzna  = 2D,  itp.), fraktale często mają wymiar ułamkowy. Przykładowo, krzywa Kocha ma wymiar ≈ 1.26, co oznacza, że jest bardziej złożona niż zwykła linia, ale nie wypełnia jeszcze płaszczyzny. Wymiar fraktalny mierzy się na różne sposoby - najpopularniejsze to wymiar samopodobieństwa, pudełkowy i Hausdorffa. Określa on liczbę skalowanych kopii potrzebnych do odtworzenia całości obiektu. Im wyższy wymiar fraktalny, tym większa złożoność i ilość informacji zawarta w strukturze. W praktyce, fraktalny wymiar wykorzystuje się w analizie obrazów, sygnałów biologicznych, linii brzegowych i danych rynkowych. W biologii pozwala ocenić złożoność układów naczyń czy neuronów. W ekonomii mierzy "chaotyczność" zmian cen i rynków. Wymiar fraktalny jest też podstawą do porównywania różnych fraktali oraz ich zastosowania w modelowaniu złożonych systemów. To narzędzie łączące geometrię z analizą rzeczywistości na wielu poziomach.

Przykłady klasycznych fraktali

Zbiór Mandelbrota

Ikoniczny obiekt w matematyce, generowany poprzez iterację funkcji zespolonej:

z_n+1=z_n²+c

gdzie z₀=0, a c jest sałą zespoloną.

jest granicą stabilności dla tej funkcji - punkty  c, dla których ciąg z_n nie ucieka do nieskończoności.

Zbiór Julii

Podobny do Mandelbrota, ale dla każdego ustalonego c badamy różne wartości z₀.

Trójkąt Sierpińskiego

Uzyskiwany przez iteracyjne usuwanie środkowych trójkątów - klasyczny przykład fraktala o wymiarze około 1.585.

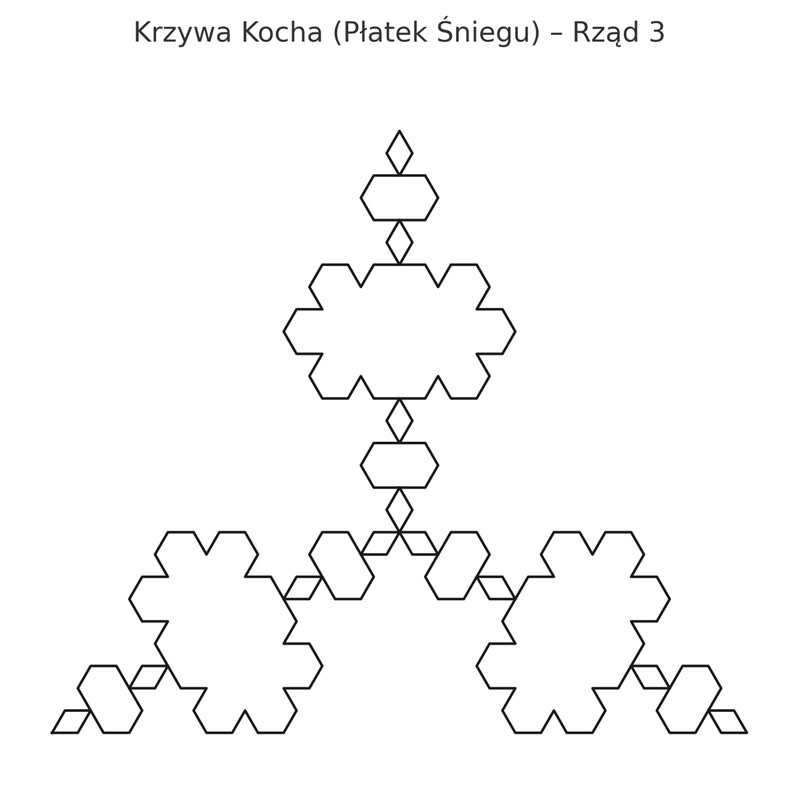
Krzywa Kocha

Tworzona przez zastępowanie odcinka trójkątem równobocznym bez podstawy. Ma nieskończoną długość i wymiar większy niż 1.

Zastosowania fraktali

Fraktale, ze względu na swoją unikalną strukturę - samopodobieństwo, nieskończoną złożoność i ułamkowy wymiar - znajdują zastosowanie w wielu dziedzinach nauki, technologii, sztuki oraz analizy danych. Poniżej przedstawiono szerokie spektrum ich zastosowań w najważniejszych obszarach współczesnej wiedzy.

Nauka i technika

Geografia i klimatologia

• Modelowanie linii brzegowych - linie brzegowe nie mają klasycznej, euklidesowej długości; są złożone i nieregularne, a ich opis geometryczny idealnie pasuje do fraktali. Mandelbrot zwrócił uwagę na ten problem pytaniem: „Jak długi jest brzeg Wielkiej Brytanii?”, pokazując, że długość ta zależy od skali pomiaru - co jest klasycznym przykładem fraktalnej natury.
• Symulacja gór i krajobrazów - fraktalne generatory terenu pozwalają na realistyczne odwzorowanie nieregularnych formacji geograficznych, takich jak łańcuchy górskie, doliny czy lodowce.
• Modelowanie chmur i zjawisk atmosferycznych - struktury chmur mają fraktalną naturę, co wykorzystywane jest w prognozowaniu pogody oraz generowaniu wizualizacji atmosferycznych w grafice komputerowej.

Biologia i medycyna

• Systemy krążenia i oddechowe - układ naczyń krwionośnych i oskrzeli ma strukturę drzewiastą, silnie samopodobną. Fraktale pozwalają modelować i analizować efektywność transportu tlenu, leków czy substancji odżywczych.
• Struktura drzew i roślin - rozgałęzienia gałęzi, korzeni, a nawet kształt liści wykazują właściwości fraktalne. Modele fraktalne są wykorzystywane do analizy wzrostu roślin i optymalizacji fotosyntezy.
• Anatomia i diagnostyka - fraktalna analiza obrazów medycznych (np. mammografii, tomografii komputerowej) pozwala wykrywać zmiany nowotworowe na podstawie analizy nieregularnych struktur w tkankach. Fraktalny wymiar może być markerem złośliwości guza.
• Neurobiologia - fraktalna architektura mózgu (rozgałęzienia dendrytów, wzorce aktywności neuronów) pomaga w zrozumieniu przetwarzania informacji i tworzenia modeli sztucznej inteligencji.

Fizyka i chemia

• Zjawiska chaotyczne i nieliniowe - fraktale opisują atraktory w układach dynamicznych, które są deterministyczne, ale zachowują się chaotycznie. Przykłady obejmują obieg atmosferyczny, ruchy cząsteczek w cieczy czy dynamikę populacji.
• Turbulencje i przepływy - struktury fraktalne pomagają opisać wieloskalowość turbulencji w płynach i gazach. Równania Naviera-Stokesa wykazują rozwiązania o fraktalnej strukturze, co jest nadal przedmiotem intensywnych badań.
• Chemia powierzchni i reakcje katalityczne - powierzchnie porowate (np. węgiel aktywny, tlenki metali) mają strukturę fraktalną, co wpływa na kinetykę adsorpcji i katalizy.

Geologia i nauki o Ziemi

• Struktura skał i złóż - porowatość i układ szczelin w skałach wykazują fraktalną geometrię, co ma znaczenie w geofizyce, hydrogeologii i eksploatacji złóż ropy czy gazu.
• Rozmieszczenie trzęsień ziemi i wulkanów - fraktalne modele pozwalają lepiej rozumieć rozkład i intensywność wstrząsów tektonicznych, a także prognozować zagrożenia sejsmiczne.
• Erozja i sedymentacja - procesy geologiczne mają charakter iteracyjny i samopodobny, co umożliwia modelowanie ewolucji krajobrazu na różnych skalach czasowych i przestrzennych.

Informatyka i grafika komputerowa

Generowanie realistycznych krajobrazów i światów wirtualnych

Algorytmy fraktalne: Perlin noise, Midpoint Displacement, Diamond-Square, są szeroko wykorzystywane w grach komputerowych, filmach i symulatorach do generowania:

• górskich krajobrazów,
• drzew i roślin,
• chmur i atmosfery,
• powierzchni planet i oceanów.

Fraktale pozwalają zachować realizm przy minimalnej ilości danych wejściowych, co jest szczególnie istotne w przypadku grafiki proceduralnej.

Fraktalna kompresja danych i obrazów

Fraktalna kompresja wykorzystuje samopodobieństwo fragmentów obrazu - zamiast zapisywać każdy piksel, zapisuje się transformacje geometryczne opisujące podobieństwa między fragmentami. Metoda ta oferuje bardzo wysokie współczynniki kompresji, szczególnie dla obrazów o dużej ilości detali, choć jej złożoność obliczeniowa ograniczyła powszechne zastosowanie.

Sztuka komputerowa i generatywna

Fraktale stały się ważnym elementem sztuki generatywnej - z ich pomocą artyści tworzą obrazy, animacje i struktury o nieskończonej głębi i symetrii.

Przykłady obejmują:

• modyfikacje zbiorów Julii i Mandelbrota w 2D i 3D,
• animacje podróży przez fraktale,
• interaktywne aplikacje artystyczne generujące fraktalne ornamenty i mandale.

Cyberbezpieczeństwo i kryptografia

Fraktale są badane jako potencjalna baza dla algorytmów kryptograficznych - dzięki swojej złożoności i trudności odwracania transformacji mogą znaleźć zastosowanie w nowych metodach szyfrowania.

Rozpoznawanie wzorców i przetwarzanie sygnałów

Analiza fraktalna znajduje zastosowanie w identyfikacji tekstur, klasyfikacji sygnałów biologicznych (np. EKG), wykrywaniu anomalii w danych czasowych oraz w machine learningu jako cecha opisująca złożoność danych.

Finanse i ekonomia

Fraktale na rynkach finansowych

Ceny akcji, indeksów giełdowych i walut wykazują samopodobieństwo - struktury cenowe na wykresach dziennych, godzinowych i minutowych mają podobne wzorce. Fraktalny charakter rynków finansowych został spopularyzowany przez Benoîta Mandelbrota, który twierdził, że tradycyjna statystyka (np. rozkład normalny) nie oddaje ekstremalnych zdarzeń i "grubych ogonów".

Modelowanie niestacjonarności i zmienności

Fraktalna geometria jest stosowana w:

• analizie zmienności rynkowej,
• prognozowaniu trendów i cykli koniunkturalnych,
• detekcji baniek spekulacyjnych i punktów krytycznych.

Teoria chaosu w finansach

W połączeniu z teorią chaosu, fraktale służą do analizy systemów nieliniowych, które są wrażliwe na warunki początkowe, lecz deterministyczne - co umożliwia szukanie ukrytego porządku w pozornie losowych szeregach czasowych.

Zarządzanie ryzykiem i portfelem inwestycyjnym

Modele fraktalne pomagają lepiej oszacować ryzyko inwestycji - zwłaszcza w kontekście nagłych, dużych fluktuacji, które nie są dobrze opisywane przez klasyczne modele oparte na średnich i odchyleniach standardowych.

Fraktale a chaos

Fraktale i chaos są ze sobą ściśle powiązane, choć na pierwszy rzut oka mogą wydawać się przeciwieństwami. Chaos kojarzy się z nieprzewidywalnością, a fraktale z uporządkowaną, choć złożoną strukturą. Jednak w rzeczywistości wiele układów chaotycznych - mimo pozornego bałaganu - tworzy fraktalne wzory w przestrzeni fazowej. Przykładem tego są tzw. atraktory dziwne, jak atraktor Lorenza, które mają strukturę fraktalną i reprezentują zachowanie systemu w czasie. Tego rodzaju atraktory nie powtarzają się dokładnie, ale mają charakterystyczny, stabilny kształt. To właśnie dzięki fraktalom możemy wizualizować i analizować chaos jako zjawisko posiadające ukryty porządek.

Fraktale często powstają z iteracji prostych równań, które wykazują chaotyczne zachowanie przy pewnych parametrach. Tak działa m.in. zbiór Mandelbrota, który mapuje stabilność układów dynamicznych. Brzegi tego zbioru są fraktalne i reprezentują granicę między porządkiem a chaosem. Samopodobieństwo fraktali znajduje odzwierciedlenie w zachowaniu układów dynamicznych, gdzie wzorce powtarzają się na różnych skalach czasowych. Chaos deterministyczny oznacza, że system działa według reguł, ale jest wrażliwy na minimalne zmiany początkowe. Mimo tej wrażliwości, jego trajektorie nie są przypadkowe - układają się w złożone fraktalne struktury. Dzięki temu fraktale są narzędziem do badania dynamiki zjawisk trudnych do przewidzenia. Umożliwiają lepsze rozumienie systemów nieliniowych, np. w meteorologii, biologii, ekonomii. Fraktale pokazują, że chaos nie jest pozbawiony porządku - jest po prostu porządkiem ukrytym w złożoności.

Programowanie fraktali

Współczesne języki programowania, takie jak Python, C++, JavaScript, Java czy Processing, pozwalają na tworzenie fraktali zarówno do celów naukowych, jak i artystycznych. Dzięki rozwojowi bibliotek graficznych, obliczeń numerycznych i przeglądarek internetowych, programowanie fraktali stało się dostępne dla szerokiego grona twórców, badaczy i hobbystów.

Podejścia algorytmiczne

Fraktale programuje się zazwyczaj przy użyciu jednego (lub kilku) z trzech głównych podejść:

• rekursja - np. dla trójkąta Sierpińskiego, krzywej Kocha czy dywanu Sierpińskiego, kod wywołuje sam siebie dla mniejszych podproblemów;
• iteracja - używana np. w tworzeniu zbiorów Julii i Mandelbrota; bazuje na powtarzaniu prostych operacji matematycznych (np. iteracja zespolonych równań kwadratowych);
• układy dynamiczne - fraktale są traktowane jako wizualizacja ewolucji stanu systemu w czasie, np. poprzez analizę trajektorii w przestrzeni fazowej.

Środowiska i narzędzia

• Python + matplotlib/PIL - świetny do analizy naukowej i szybkiej prototypizacji.
• JavaScript + HTML5 Canvas - umożliwia tworzenie interaktywnych fraktali działających w przeglądarce.
• C++/OpenGL - przydatny przy tworzeniu szybkich, zaawansowanych wizualizacji 2D i 3D.
• Processing / p5.js - środowiska stworzone dla artystów i projektantów wizualnych.

Przykład - Trójkąt Sierpińskiego w języku JavaScript (Canvas)

Poniższy kod tworzy fraktalny trójkąt Sierpińskiego za pomocą HTML i JavaScript w przeglądarce, korzystając z metody chaosu (losowej iteracji):

<!DOCTYPE html>
<html>
<head>
  <meta charset="UTF-8">
  <title>Trójkąt Sierpińskiego</title>
  <style>
    canvas { background: #111; display: block; margin: auto; }
  </style>
</head>
<body>
<canvas id="fractalCanvas" width="600" height="600"></canvas>

<script>
  const canvas = document.getElementById("fractalCanvas");
  const ctx = canvas.getContext("2d");
  const width = canvas.width;
  const height = canvas.height;

  // Wierzchołki trójkąta
  const A = [width / 2, 20];
  const B = [20, height - 20];
  const C = [width - 20, height - 20];

  // Ustawienia punktów
  let x = Math.random() * width;
  let y = Math.random() * height;

  ctx.fillStyle = "lime";

  function drawPoint(x, y) {
    ctx.fillRect(x, y, 1, 1);
  }

  // Algorytm chaosu
  for (let i = 0; i < 50000; i++) {
    const vertex = [A, B, C][Math.floor(Math.random() * 3)];
    x = (x + vertex[0]) / 2;
    y = (y + vertex[1]) / 2;
    drawPoint(x, y);
  }
</script>
</body>
</html>

Omówienie działania programu

• Na początku definiowane są trzy wierzchołki trójkąta równobocznego.
• Losowo wybierany jest punkt startowy.
• W każdej iteracji wybierany jest losowy wierzchołek, a punkt przesuwany jest w jego kierunku o połowę odległości.
• Rysowany jest nowy punkt - z czasem wyłania się struktura trójkąta Sierpińskiego.

Badania nad fraktalami

Zastosowania fraktali rozwijają się dynamicznie:

• fraktalna analiza danych w uczeniu maszynowym,
• modele sieci neuronowych oparte na fraktalnych strukturach,
• zastosowania w medycynie (rozpoznawanie nowotworów po fraktalnych wzorcach),
• nowe algorytmy kryptograficzne.

Fraktale to pomost między matematyką, przyrodą i sztuką. Łączą w sobie prostotę zasad z nieograniczoną złożonością efektów. Ich badanie nie tylko dostarcza narzędzi do modelowania świata rzeczywistego, ale także głębszego wglądu w struktury ukryte we wszechświecie. W świecie, gdzie chaos i porządek współistnieją, fraktale pokazują, że piękno i logika mogą wyrastać z najprostszych reguł.

FAQ - Fraktal