Histogram - definicja, tworzenie, rodzaje, zastosowania, przykłady
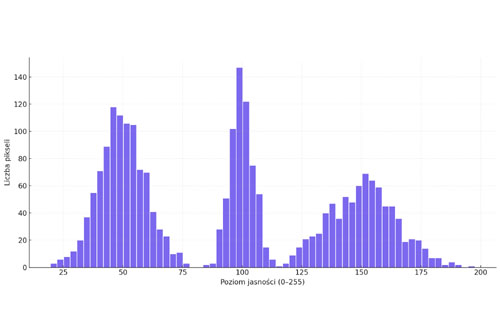Histogram to jedno z najbardziej podstawowych, a zarazem niezwykle potężnych narzędzi analizy danych. Choć jego konstrukcja jest prosta, dostarcza ogromnej ilości informacji o rozkładzie danych, strukturze populacji, zmienności i tendencjach. Znajduje zastosowanie nie tylko w statystyce, ale także w informatyce, przetwarzaniu obrazów, uczeniu maszynowym, fizyce, biologii, ekonomii i niemal każdej dziedzinie analizy danych ilościowych.
Definicja histogramu
Histogramy mogą być używane do wizualizacji danych ciągłych (np. pomiary temperatury) lub dyskretnych (np. liczba dzieci w rodzinach).
Histogram vs. wykres słupkowy - różnice
Choć histogram i wykres słupkowy wyglądają podobnie, mają zasadnicze różnice.
| Cecha | Histogram | Wykres słupkowy |
|---|---|---|
| Dane | Liczbowe, ciągłe | Kategoryczne |
| Oś X | Przedziały liczbowe (ciągłość) | Kategoria (np. kraj, kolor, typ) |
| Odstępy między słupkami | Brak (przylegające) | Obecne |
| Interpretacja | Rozkład wartości | Porównanie kategorii |
Znaczenie i zastosowania histogramów
Statystyka i analiza danych
- Ocena rozkładu zmiennej (czy dane są symetryczne, skośne, normalne),
- Wykrywanie wartości odstających (outliers),
- Szacowanie parametrów statystycznych (średnia, mediana, wariancja),
Przetwarzanie obrazów
- Histogramy intensywności (np. poziomu jasności w obrazie),
- Normalizacja i rozciąganie histogramu (histogram equalization),
- Detekcja kontrastu i analiza kolorów.
Uczenie maszynowe i AI
- Inżynieria cech (feature engineering) - histogramy jako wektory cech,
- Klasyfikacja obrazów (np. histogramy gradientów - HOG),
- Analiza rozkładu zmiennych w zbiorze treningowym.
Finanse i ekonomia
- Analiza rozkładu zwrotów inwestycji,
- Wykrywanie anomalii w transakcjach.
Nauki przyrodnicze i medyczne
- Histogramy sygnałów biologicznych (np. EKG, EEG),
- Rozkład rozmiarów cząstek, liczby komórek, intensywności fluorescencji.
Tworzenie histogramu
Jak powstaje histogram?
- Dany zbiór liczbowy (np. wyniki testów, temperatury, wartości pomiarów) można przedstawić graficznie, dzieląc go na grupy wartości o określonej szerokości - tzw. przedziały klasowe lub kosze (bin’y).
- Zakres danych dzieli się na równe przedziały, np. 0-10, 10-20, 20-30 itd.
- Następnie zlicza się, ile wartości mieści się w każdym przedziale.
- Dla każdego przedziału rysuje się słupek - im więcej wartości w danym zakresie, tym wyższy słupek.
W ten sposób tworzony jest histogram pokazujący rozkład danych. Wersja pokazująca procentowy udział wartości w każdej klasie nazywana jest właśnie histogramem względnym.
Dobór liczby grup (binów)
Wybór liczby przedziałów ma wpływ na czytelność wykresu:
- zbyt mała liczba przedziałów prowadzi do uproszczenia danych i utraty szczegółów.
- zbyt duża liczba sprawia, że histogram staje się "zaszumiony" i trudniejszy do interpretacji.
W praktyce stosuje się proste reguły doboru liczby binów, zależne od liczby danych lub ich rozrzutu.
Reguła Sturgesa
Liczba grup k obliczana jest według wzoru:
k=[log2(n)+1]
gdzie n to liczba danych. Reguła ta dobrze sprawdza się dla małych i średnich zbiorów.
Reguła Freedmana-Diaconisa
Używana, gdy dane mają duży rozrzut. Szerokość h binu wyznaczana jest jako:
h=2⋅IQR/(pierwiastek 3 stopnia z (n))
gdzie IQR to rozstęp międzykwartylowy, a n to liczba obserwacji.
Interpretacja kształtu histogramu
Kształt histogramu może sugerować typ rozkładu i właściwości zmiennej:
| Kształt | Znaczenie |
|---|---|
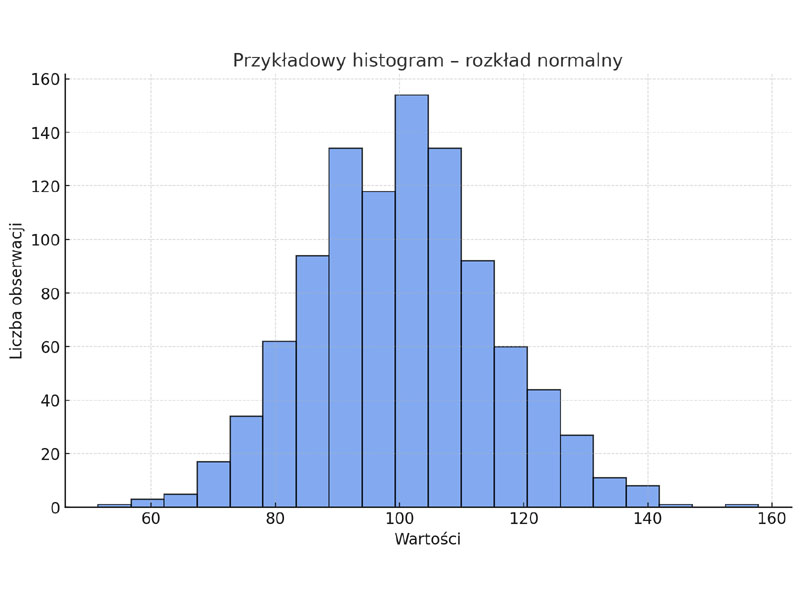
| Symetryczny | Rozkład normalny, brak skośności |
| Skośny w prawo | Więcej wartości małych, długi ogon prawy |
| Skośny w lewo | Więcej wartości dużych, długi ogon lewy |
| Dwumodalny | Dwie dominujące grupy (np. dwie populacje) |
| Spłaszczony | Rozkład bardziej rozproszony niż normalny |
| Wąski | Dane silnie skupione |
Rodzaje histogramów
Istnieje kilka wariantów histogramów, które mają swoje konkretne zastosowania, szczególnie w analizie porównawczej, przetwarzaniu obrazów, statystyce wielowymiarowej i eksploracji danych.
Histogram względny (częstościowy)
Opis
Histogram względny zamiast przedstawiać liczbę obserwacji w każdym przedziale (binie), prezentuje częstość względną, czyli procentowy udział danej klasy w całkowitej liczbie danych.
Zastosowania
- Porównywanie dwóch lub więcej zbiorów danych o różnej liczności (np. grupa A = 500 osób, grupa B = 2000 osób),
- Analiza proporcji bez względu na skalę absolutną (np. udział przedziałów wiekowych w różnych populacjach),
- Przygotowanie danych do wykresów porównawczych (np. wykresy skumulowane lub warstwowe).
Przykład
Jeśli w danym przedziale znajduje się 50 obserwacji z 1000, to słupek ma wysokość 0.05 (5%).
Histogram skumulowany (cumulative histogram)
Opis
W histogramie skumulowanym każdy kolejny słupek przedstawia sumę wszystkich wcześniejszych wartości wraz z aktualnym przedziałem. Taki wykres reprezentuje funkcję rozkładu empirycznego (EDF).
Zastosowania
- Wyznaczanie kwantyli (np. mediana = wartość dla której skumulowana częstość osiąga 50%),
- Ocena dystrybucji danych i ich rozkładu (szukanie momentu, w którym dane gwałtownie rosną),
- Porównania statystyczne - np. testy Kolmogorowa-Smirnowa.
Przykład
Jeśli trzy pierwsze biny mają odpowiednio 10, 15 i 20 obserwacji, to ich wartości skumulowane to 10, 25, 45.
Histogramy 2D i 3D (joint histograms)
Opis
Histogramy 2D (lub 3D) przedstawiają wspólny rozkład dwóch lub trzech zmiennych jednocześnie. Oś X reprezentuje jedną zmienną, oś Y drugą, a wysokość lub kolor słupka - liczbę współwystąpień danej pary wartości.
Zastosowania
- Analiza współzależności zmiennych - np. związek wzrostu i masy ciała,
- Przetwarzanie obrazów: wspólna analiza jasności i kontrastu, histogramy kanałów RGB, dopasowanie kolorów,
- Statystyka wielowymiarowa: badanie korelacji i zależności w dużych zbiorach danych.
Przykład
Histogram 2D może przedstawiać, ile pikseli ma daną kombinację jasności i kontrastu - pozwala to np. na korekcję oświetlenia obrazu.
Histogramy normalizowane
Opis
Histogramy normalizowane mają słupki przeskalowane tak, aby całkowita suma powierzchni wynosiła 1. Dzięki temu histogram może być traktowany jako przybliżenie funkcji gęstości rozkładu.
Zastosowania
- Porównywanie rozkładów prawdopodobieństwa dla różnych prób,
- Wykorzystanie histogramów jako wejścia do algorytmów uczenia maszynowego (np. SVM, klasyfikacja obrazów),
- Wizualizacja danych jako ciągłych rozkładów (gładkie krzywe, funkcje gęstości).
Różnica względem histogramu względnego
Histogram względny pokazuje proporcje (słupki sumują się do 1), ale nie uwzględnia szerokości binów. Histogram normalizowany uwzględnia zarówno liczbę obserwacji, jak i szerokość przedziału, co sprawia, że obszar pod wykresem odpowiada całkowitemu prawdopodobieństwu = 1.
Porównanie rodzajów histogramów
| Rodzaj histogramu | Co pokazuje | Do czego służy |
|---|---|---|
| Zwykły (częstości) | Liczba obserwacji | Klasyczna analiza rozkładu danych |
| Względny (częstościowy) | Procentowy udział | Porównanie rozkładów o różnych rozmiarach |
| Skumulowany | Narastająca suma wartości | Analiza kwantyli, estymacja funkcji rozkładu |
| 2D / 3D (joint) | Współwystępowanie zmiennych | Analiza korelacji, przetwarzanie obrazów |
| Normalizowany | Gęstość rozkładu (obszar = 1) | Estymacja PDF, analiza ciągłych danych |
Programowanie i tworzenie histogramów
Histogramy można generować za pomocą wielu narzędzi i języków programowania, np.:
(Python + OpenCV)
import cv2
import matplotlib.pyplot as plt
img = cv2.imread('image.jpg', 0) # obraz w skali szarości
hist = cv2.calcHist([img], [0], None, [256], [0, 256])
plt.figure(figsize=(8, 4))
plt.title("Histogram obrazu (skala szarości)")
plt.plot(hist, color='gray')
plt.xlabel("Wartości pikseli")
plt.ylabel("Liczba pikseli")
plt.grid(True, linestyle='--', alpha=0.4)
plt.show()
Histogramy w przetwarzaniu obrazów
W przetwarzaniu obrazów histogramy służą nie tylko do analizy rozkładu jasności lub kolorów, ale także do aktywnego przekształcania obrazu w celu poprawy jego jakości i czytelności. Dają one prosty sposób na zrozumienie struktury wizualnej obrazu, a także umożliwiają zastosowanie efektywnych metod korekty, dopasowania i segmentacji.
Histogram equalization (wyrównywanie histogramu)
To technika poprawiająca kontrast obrazu przez przekształcenie jego histogramu tak, by rozkład poziomów jasności był bardziej równomierny. Dzięki temu obraz staje się bardziej czytelny - jasne obszary są rozjaśniane, ciemne pogłębiane, a szczegóły bardziej widoczne. Jest to powszechnie stosowane w obrazach rentgenowskich, satelitarnych czy przy słabym oświetleniu.
Histogram matching (dopasowanie histogramu)
Polega na przekształceniu histogramu jednego obrazu tak, aby upodobnił się do histogramu innego (wzorcowego). Stosuje się go np. w przetwarzaniu wideo, gdzie zachowanie spójności kolorystycznej między klatkami lub scenami jest kluczowe. Pomaga też w analizie obrazów pochodzących z różnych źródeł o różnym oświetleniu.
Segmentacja obrazów (thresholding)
Histogram obrazu umożliwia szybkie wykrycie progów, które oddzielają obiekty od tła. W najprostszej wersji stosuje się jeden próg jasności, dzieląc piksele na ciemne i jasne. Bardziej zaawansowane metody, jak algorytm Otsu, automatycznie znajdują wartość progu minimalizującą niejednorodność w obrazie. To podstawa do dalszego przetwarzania, np. wykrywania krawędzi czy rozpoznawania obiektów.
Przykład
W obrazach czarno-białych histogram pokazuje rozkład poziomów szarości (0-255). Obrazy o niskim kontraście mają wąski histogram skupiony w jednym zakresie.
Analiza histogramu - przykład
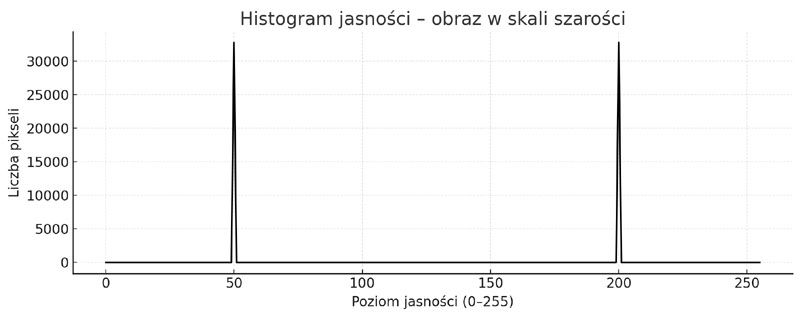
Powyższy wykres przedstawia histogram jasności dla sztucznie utworzonego obrazu w skali szarości, podzielonego na dwie równe części: ciemną (poziom szarości = 50) i jasną (poziom szarości = 200).
Opis histogramu
- Oś X przedstawia poziomy jasności od 0 (czarny) do 255 (biały)
- Oś Y pokazuje liczbę pikseli odpowiadających każdemu poziomowi
- W histogramie widać dwa wyraźne piki:
- jeden przy poziomie 50 - odpowiada lewej, ciemnej połowie obrazu,
- drugi przy poziomie 200 - odpowiada prawej, jasnej połowie.
Poziomy pomiędzy (np. 100, 150) są puste, ponieważ w obrazie nie występują piksele o tych wartościach.
Wnioski
Histogram pozwala od razu zrozumieć, że obraz zawiera tylko dwa zakresy jasności.
Jest to przykład dwumodalnego rozkładu jasności, typowego np. dla obrazów binarnych, podzielonych lub segmentowanych.
Histogram tego typu świetnie nadaje się do progującej segmentacji obrazu.
Histogram to jedno z najważniejszych narzędzi eksploracji danych. Łączy prostotę wykonania z głębią interpretacyjną, dając wgląd w naturę zmiennych, rozkład obserwacji i właściwości próbki. Znajduje zastosowanie w niemal każdej dziedzinie, gdzie analizowane są dane ilościowe: od nauki, przez inżynierię i ekonomię, aż po sztuczną inteligencję i grafikę komputerową. Jego poprawna konstrukcja i interpretacja są podstawą każdej rzetelnej analizy statystycznej.
Komentarze